Nawet jeśli nie przepadasz za matematyką, pokaż dziecku jej piękno, aby z przyjemnością i łatwością się jej w przyszłości uczyło. Idealnie nadaje się do tego geometria i na przykład jedna z brył foremnych: dwunastościan. Możemy kolorować jej siatkę, tworząc kwiaty, szukać na obrazach Salvadora Dali lub podziwiać ją w nowoczesnej kamerze, albo wśród rzymskich zabytków.
Na szkoleniu Wczesna nauka matematyki omawialiśmy, jak codziennie przez kilka sekund dziennie prezentować dzieciom działania matematyczne. Warto zacząć tak wcześnie, jak to tylko możliwe, póki nie wygasną naturalne wrodzone zdolności matematyczne, które posiada każde zdrowe dziecko,
To wystarczy, aby w przyszłości algebra była dla dziecka łatwa. Ale może nie wystarczyć aby pokochało matematykę i uczyło się jej z pasją. Dlatego wspierajmy nasze codzienne kilkusekundowe prezentacje – opowiadajmy dziecku o pięknie matematyki, które można dostrzec niemal w każdym zakątku otaczającego nas świata.
Opowieści matematyczne o bryłach foremnych
W pierwszej części poznaliśmy słownictwo dotyczące figur i brył, jako wstęp do opowiadania o najpiękniejszych bryłach, wielościanach foremnych, które z racji swojego piękna i regularności zwiemy bryłami platońskimi.
Sześcian – jako najpopularniejsza bryła – rozpoczął naszą przygodę z wielościanami foremnymi. Kliknij w link, aby przejść do artykułu o sześcianie.
W części drugiej zbudowaliśmy najmniejszą bryłę platońską czyli czworościan foremny i rozwiązywaliśmy zagadki o nim. Dowiedzieliśmy się, gdzie w naturze i kosmosie możemy spotkać czworościan foremny oraz jak o nim mówił Platon. Kliknij w link, aby przejść do artykułu o czworościanie foremnym.
Natomiast w części trzeciej zbudowaliśmy ośmiościan, kształt który najczęściej przyjmuje diament. Kliknij w link, aby przejść do artykułu o ośmiościanie.
Dziś zbudujemy czwartą bryłę foremną – dwunastościan.
Budujemy dwunastościan
Ośmiościan foremny ma osiem ścian (jak wskazuje nazwa). Zbudowany jest z trójkątów równobocznych – podobnie jak czworościan.



Powyższy ośmiościan zbudowany jest z magnetycznych pałeczek, metalowych kuleczek i plastykowych ścian, które wchodzą w skład kloców Geomag.
Popatrzmy na niego z różnych stron, a nawet zróbmy mu zdjęcia aparatem w telefonie, aby dostrzec piękne regularności.

Na zdjęciu widać, że kiedy położymy go na stole, to dolna i górna podstawa będą równoległe. Każda z nich otoczona jest przez wianuszek pięciu ścian bocznych. Moglibyśmy nawet rozłożyć dwunastościan na dwie misy zbudowane z podstawy i pięciu ścian bocznych.
Poznajemy dwunastościan
Ile krawędzi ma dwunastościan? Ile wierzchołków ma dwunastościan? A ile ma ścian? – zadajmy te pytania dziecku, o ile jest szansa, że będzie potrafiło na nie odpowiedzieć. Jeśli nie, to sami opowiedzmy maluszkowi o jego właściwościach.
Dwunastościan ma 12 ścian, 30 krawędzi i 20 wierzchołków.
Właściwości dwunastościanu
Spełnia on trzy podstawowe warunki, jakie musi spełniać każdy wielościan foremny.
- Każda ściana jest takim samym (przystającym) wielokątem foremnym – w szczególności ściany są pięciokątami foremnymi – taki pięciokąt ma wszystkie boki równe i wszystkie kąty równe. Kąty w pięciokącie równobocznym mają po 108 stopni.
- W każdym wierzchołku zbiega się taka sama liczba ścian: trzy ściany. Dodatkowo w każdym wierzchołku zbiega się taka sama liczba krawędzi: również trzy.
- Dwunastościan foremny jest bryłą wypukłą, czyli nie jest zapadnięty.
Po angielsku 12-ścian nazywamy dodecahedron.
Siatka dwunastościanu
Siatka dwunastościanu tworzy dwa piękne kwiaty.
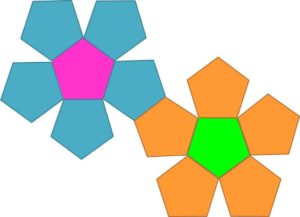
Przekątne dwunastościanu
Dwunastościan foremny ma aż 100 przekątnych wewnętrznych. Dodatkowo można policzyć przekątne ścian – jest ich 60 (12 razy po pięć).
Historia dwunastościanu
Ostatni z odkrytych
Dwunastościan został odkryty jako ostatni. Wbrew powszechnym przekonaniom, wielościanów foremnych jest skończona liczba – jest ich raptem pięć. To Platon jako pierwszy odnotował fakt istnienia ściśle określonej ich liczby. Do jego czasów znano ich jedynie cztery. Ostatni, piąty wielościan foremny – dwunastościan – został odkryty przez ucznia Platona – Teajtetosa.
Symbol wszechświata
W dialogu “Timajos” Platon pisał, że każdy żywioł można utożsamić z jedną z doskonałych brył (ogień – czworościan, ziemia – sześcian, powietrze – ośmiościan, woda – dwudziestościan).
Choć Platon nie znał dwunastościanu, postulował jego istnienie i uważał, że ta piąta z brył jest symbolem całego wszechświata.
Boska matematyka
Niemal 2 tysiące lat później, w XVII wieku Kepler użył wielościanów foremnych do swojego modelu kosmologicznego. Dwunastościan można wpisać między dwie sfery wyznaczone przez orbity Ziemi i Marsa.
Kepler zauważył zależność: na sferze o promieniu orbity Merkurego można opisać ośmiościan. Jeśli na nim opisać następną sferę, to jej promień odpowiadać będzie promieniowi orbity Wenus. Na tej drugiej sferze Kepler opisał dwudziestościan, a na nim kolejną trzecią sferę, po której poruszała się Ziemia. I tak kolejno dla następnych wielościanów foremnych i planet:
Merkury – ośmiościan – Wenus – dwudziestościan – Ziemia – dwunastościan – Mars – czworościan – Jowisz – sześcian – Saturn. Było to pierwsze z odkrytych przez Keplera praw ruchu planet. Odkryta prawidłowość utwierdziła Keplera w głębokim przekonaniu, że Bóg jest matematykiem.
Ciekawostki matematyczne o dwunastościanie
Porównywanie objętości
Jeśli jeszcze macie ośmiościan foremny, to możemy porównać ich objętości. Dzięki temu odpowiemy na pytanie, ile razy więcej wody można wlać do naczynia w kształcie dwunastościanu foremnego niż do naczynia w kształcie ośmiościanu foremnego o takiej samej długości krawędzi.
Ponad 16 razy więcej.
Gdy porównamy objętość dwunastościanu i dwudziestościanu o tej samej długości krawędzi, to okaże się, że dwunastościan ma objętość ponad trzy i pół raza większą.
Objętościowa ciekawostka
Gdyby wszystkie pięć wielościanów foremnych zbudować w taki sposób, aby ich krawędzie miały te same długości – czyli tak, jak zrobiliśmy to przy użyciu Geomaga – to dwunastościan miałby największą objętość.
Zatem gdyby zbudować wszystkie pięć wielościanów foremnych o tej samej objętości, to dwunastościan miałby najkrótsze krawędzie.
Jak bracia
- Dwunastościan foremny ma 12 ścian – oczywiście – i 20 wierzchołków.
- Tymczasem dwudziestościan foremny ma 20 ścian – oczywiście – i 12 wierzchołków.
- Oba mają 30 krawędzi.
Dwunastościan w sztuce i kulturze
Dwunastościany rzymskie
Dwunastościan rzymski to mały wydrążony obiekt wykonany z brązu lub kamienia, o dwunastościennym kształcie: dwanaście płaskich pięciokątnych powierzchni, każda powierzchnia ma okrągły otwór o różnej średnicy w środku. Pochodzą z 2. lub 3. wieku naszej ery.

Około setki dwunastościanów znaleziono od Walii po Węgry i Hiszpanię oraz od wschodu Włoch, najwięcej w Niemczech i we Francji. W rozmiarach od 4 do 11 centymetrów (od 1,6 do 4,3 cala) różnią się również pod względem tekstury. Większość z nich jest wykonana z brązu, ale niektóre są z kamienia.
Nie znamy przeznaczenia dwunastościanów, ale wiemy, że były cenne, gdyż przechowywano je w skarbcach wraz z monetami.
Salvador Dali
W obrazie Sakrament ostatniej wieczerzy Salwador Dali umieścił Jezusa i dwunastu apostołów w dwunastościanie foremnym.

Sakrament Ostatniej Wieczerzy został ukończony podczas ery Dali po II wojnie światowej, która charakteryzuje się rosnącym zainteresowaniem nauką, złudzeniem optycznym i religią. W tym czasie stał się pobożnym katolikiem i jednocześnie był zaskoczony ” epoką atomową “.
Dali napisał:
Pierwsza Komunia Święta na Ziemi jest pomyślana jako święty obrzęd największego szczęścia dla ludzkości.
Dwunastościan w sztuce
Maurits Cornelis Escher (1898 – 1972) powszechnie znany jako MC Escher, był holenderskim grafikiem, który wykonał matematycznie inspirowane drzeworyty, litografie i mezzotinty.
W 1943 roku wydrukowana została litografia MC Eschera pod tytułem Gady, na której widać dwunastościan foremny.
Gerard Caris (ur. 20 marca 1925 r.) holenderski rzeźbiarz i artysta, oparł całą swoja twórczość na dwunastościanie i pięciokącie. Sam nazwał tworzony przez siebie kierunek w sztuce Pentagonizmem.
Kostka do gry
We współczesnych grach fabularnych regularny dwunastościan jest często używany jako dwunastościenna kostka, jedna z bardziej powszechnych kostek wielościennych. Bardzo często zamiast oczek posiadają one cyferki lub ikonki.
Kości dwunastościenne stosowana są w grze Superfarmer. Jest to polska gra, w której używa się 2 takich kości z ikonkami zwierząt zamiast cyfr lub oczek.
Kwazikryształy
Kwazikryształ to szczególna forma ciała stałego, w której zazwyczaj atomy układają się w pozornie regularną, jednak nie w powtarzającą się strukturę. Za odkrycie kwazikryształów Dan Shechtman otrzymał 5.10.2011 Nagrodę Nobla w dziedzinie chemii.
Kwazikryształy wykazują słabe przewodnictwo cieplne i elektryczne, przy zachowaniu wysokiej twardości, odporności na czynniki chemiczne i korozję. Dzięki temu stosuje się je do pokryć przeciwkorozyjnych, jako materiały do magazynowania wodoru, bariery termiczne i czujniki podczerwieni.

Kwazikryształ holmu-magnezu-cynku (Ho-Mg-Zn) jest kwazikryształem wykonanym ze stopu tych trzech metali. Ma kształt regularnego dwunastościanu, bryły platońskiej z 12 pięciokątnymi ścianami, które są prawdziwymi pięciokątami regularnymi.
Dwunastościenna kamera
Dodeca 2360 to pierwsza na świecie kamera z pełną obsługą ruchu w zakresie 360°, która rejestruje wideo w wysokiej rozdzielczości z każdego kierunku jednocześnie z szybkością ponad 100 milionów pikseli na sekundę lub 30 klatek na sekundę.
Kamera została skonstruowana na bazie dwunastościanu foremnego. Dziesięciokilogramowe urządzenie ma 12 obiektywów i rejestruje obraz z prędkością ponad 100 megapikseli na sekundę. Ponadto nagrywa ono dźwięk z czterech kierunków jednocześnie. Dzięki tej kamerze widz może sam decydować, w którym kierunku chce patrzeć. Istnieje też możliwość projekcji filmów na ogromnych kopułach.

Opisywana technologia debiutuje w świecie filmów internetowych, ale wcześniej była ona używana przez FBI podczas przygotowań do wizyt ważnych gości, a także przez Google’a podczas tworzenia serwisu Street View.
Dwunastościan w chemii
Dodekaedran to związek chemiczny z grupy węglowodorów. Został zsyntetyzowany po raz pierwszy przez Leo Paquette z Ohio State University w 1982 roku, przede wszystkim z powodu “estetycznej symetrii szkieletu dwunastościennego “. Ma wzór sumaryczny C20H20.
Poszukiwania podczas spacerów
Szukajmy dwunastościanów i innych brył czy nawet figur w otaczającym nas świecie przy okazji każdego wyjścia z domu, każdego spaceru, zakupów lub wizyty u znajomych.



Nie tylko geometria
Nauczanie geometrii może być fascynujące, dlatego jest dobrym pomysłem na lęk przed matematyką czy niechęć, którą obserwujemy u uczniów wszystkich poziomów, w każdym wieku. Warto jednak pamiętać, że wszyscy rodzimy się ze zdolnościami matematycznymi, które pozwalają na rozpoczęcie nauki algebry już od urodzenia. Trzeba tylko wiedzieć jak. Dlatego spotkajmy się na szkoleniu dla rodziców małych dzieci o wczesnej nauce matematyki.
Chcesz dowiedzieć się, jak powinna przebiegać prawidłowa wczesna nauka liczenia?
Polecane szkolenie
Polecane produkty














